Efficiently updatable neural nets for chess
When I tried to write my own chess engine, there was one thing that I tried to avoid working on for a really long time. It was the evaluation function.
The way computers play chess (sort of) is that they try out all the moves they can do and they check how good the position is for them after each move. If they eat the enemy’s queen and their score jumps from 100 to 1000, then the move was probably pretty good, so they choose it over the others.
The evaluation function is what tells computers how good a position is.
When humans (who are good at chess) look at a chess position they can tell very quickly how good the position is for each side. They don’t follow a clear procedure to decide, like counting the material or checking how many pieces enemy pieces are dangerously close to their king. They just look at the board and they make sense of it using their intuition.
We’re gonna try to encode this intuition into a program that a chess engine can run. The problem with this is that it’s a complex process that you can’t just model with a simple set of logical programmable rules. Manually creating your own evaluation function is super hard and time consuming, and also the result is usually not that good.
Let’s try anyways to give you an idea of what it would look like.
The easiest thing we can start with is adding the material. Let each piece have some score. The queen has a really big score, the pawn a little score, and the king has an infinite score, etc. So you add all the scores for each side and you subtract the score from black from the score of white.
If you want to improve it you can also assign each square a given value for each piece. If your king is in the middle of the board, that’s bad! It’s vulnerable. So for the king, the squares in the middle have a negative score. The squares on the edges have a positive score. The king is more protected on the edges. This makes sense in the early or mid-game, but not so much in the late game. Therefore you’ll need another function which will try to determine the stage.
If you want to improve on this you can also assign a score to how protected your king is. If it’s close to an enemy queen you lose points.
You can do many more improvements like these and your evaluation function will probably still be pretty bad.
You’ll need many more heuristics like these to approximate the intuition that good chess players have developed to analyze positions. You can take a look at the evaluation function from Stockfish to see how a good evaluation function looks like https://github.com/official-stockfish/Stockfish/blob/master/src/evaluate.cpp.
To make things more complicated, we also have to assign numbers to the importance of each of your heuristics. How much should it penalise to have a king in the middle of the board? 5? 15? 1000? 5 pawns?
So basically we’re trying to take a quantitative approach towards analyzing positions, but at some point we’ll just have to make up a bunch of numbers for weighting each of your heuristics, which isn’t really that quantitative.
The only way to get these parameters closer to optimal is through testing and carefully tweaking your parameters (or using Texel tuning!).
But there’s an easier way which works better…
A neural network!
Why not replace our classical manually crafted evaluation function with a neural network?
Sounds reasonable! And it is in fact a great idea. It turns out that neural nets can approximate optimal evaluation functions pretty well. But there is one big problem that has to be overcome, which is sort of unique for chess engines. We have to make our network fast to run.
To give you an idea: a good chess engine might evaluate >10 million positions per second. The more positions it can search, the deeper it can go into each position to simulate how good the initial move was.
You might have a good neural network, which has a deep understanding of how good a chess position is, but it might be much worse than having a very dumb but very fast evaluation function like the one we saw before. So the question isn’t “What’s the architecture that will minimize my loss” but rather “What’s the architecture that perfectly balances speed with minimizing my loss”.
A Japanese guy called Yu Nasu found a good answer to this question in 2018. He invented something called an efficiently updatable neural network, which is abbreviated as NNUE because it sounds way cooler than EUNN. He published his idea in a paper, which you can find here.
The paper is in Japanese (english one here) and it actually wasn’t meant for chess, it was meant for Shogi. But it turns out that the algorithm worked incredibly well for chess too. In August 2020 the 12th version of Stockfish was released and it used an NNUE per default. They claim that it increased ELO by 100 points, which is a huge success considering that modern chess engines are approaching perfection.
So let’s see why NNUE is fast and good.
Here’s a picture from chessprogramming which illustrates the high-level architecture.
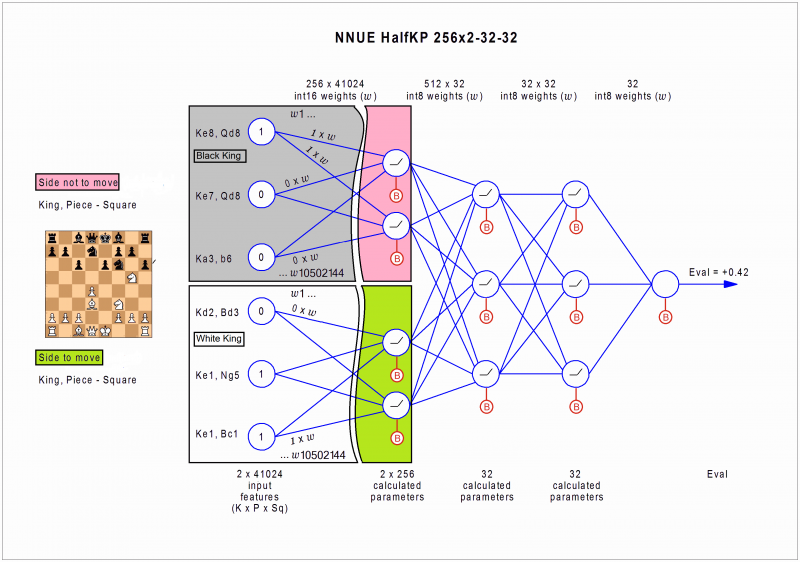
Our neural network is essentially a function which has a board as an input and a numerical score (an integer) as an output.
We can think of our network as being a function, which receives a Board and returns an integer representing the score.
We’re going to break down this function into its three main components and understand each one of them in detail.
def evaluation(Board):
active_indices = compute_active_indices(board)
accumulator = compute_accumulator(active_indices)
output = run_network(accumulator)
return output
The first function creates a list of indices. Each one of them tells us that certain weights should be added to our accumulator, which is just two big arrays of 256 elements. Then we feed the accumulator into our network.
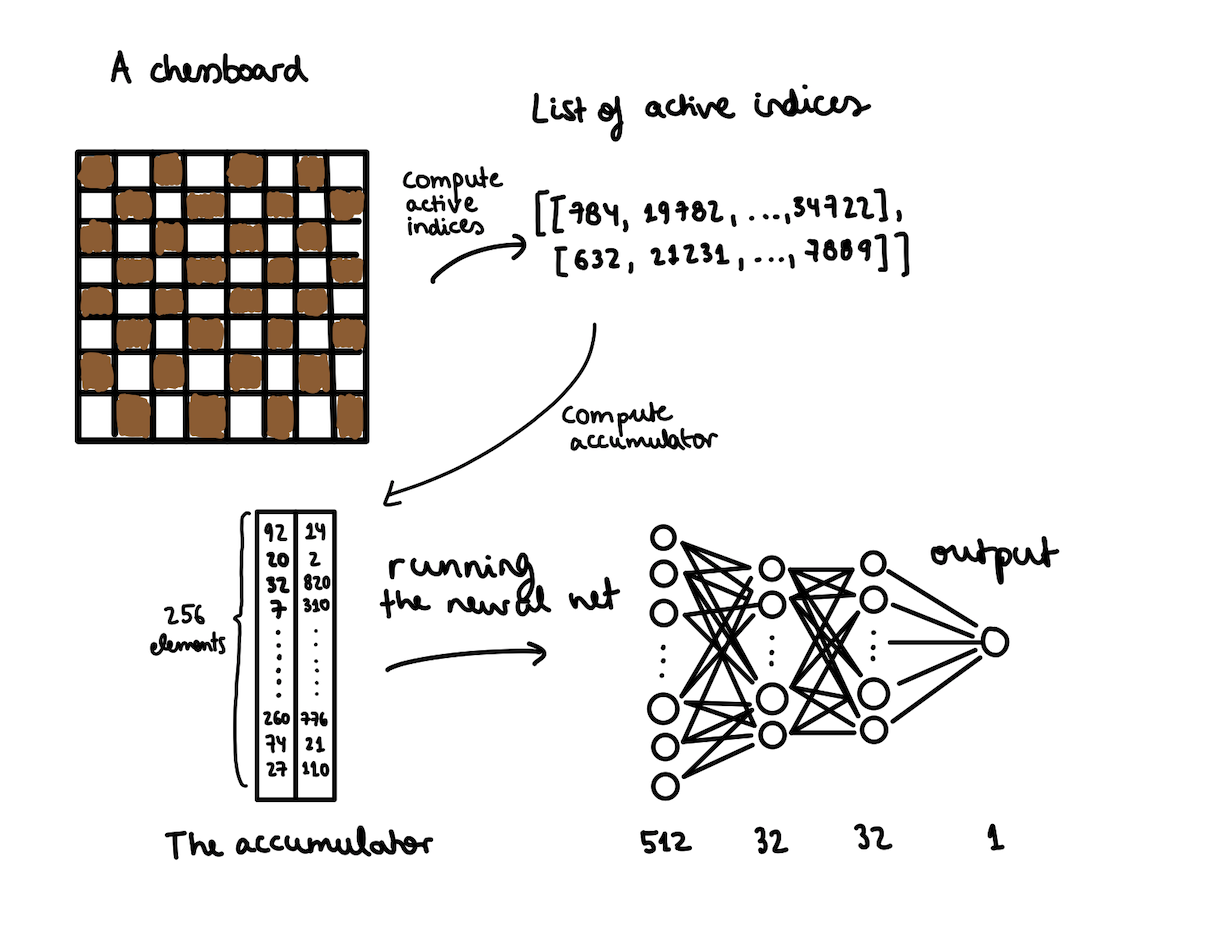
Let’s dive into the first component.
The active indices
This function will be passed a Board object, containing the positions of each piece in the board, and it will return two lists of integers, one for white and one for black. Each number in the list represents an index in a big array of weights. We’ll look at this indices in detail later, but basically each index tells us that certain weights should be activated to fill in our accumulator.
Let’s just look at the implementation and then I’ll discuss what’s happening. Before that, let me also say that the way I query my board is using board.piece[square] and board.color[square], whereas square is an integer between 0 and 63. Also, the pieces are named in increasing order WHITE_PAWN = 0, WHITE_KNIGHT = 1, WHITE_BISHOP = 2, WHITE_ROOK = 3, WHITE_QUEEN = 4, WHITE_KING = 5, BLACK_PAWN = 6, …, BLACK_KING = 11. If you’re trying to put an NNUE into your engine, then you’d have to adapt this function to your own board representation. It shouldn’t be too hard.
piece_to_index = [[ 1, 129, 321, 449, 577, 0, 65, 257, 385, 513, 641, 0],
[65, 257, 385, 513, 641, 0, 1, 129, 321, 449, 577, 0]]
def calculate_index(piece, color, square,
white_king_square, black_king_square,
perspective):
if perspective == WHITE:
return sq + piece_to_index[WHITE][piece] + (white_king_square * INDEX_END)
elif perspective == BLACK:
return (sq ^ 63) + piece_to_index[BLACK][piece] + (black_king_square * INDEX_END)
def compute_active_indices(board):
white_king_square = board.get_white_king_square()
black_king_square = (board.black_king_square ^ 63)
for square in range(64):
if board.piece[square] != EMPTY and board.piece[square] != KING:
white_indices.append(
calculate_index(board.piece[square], board.color[square], square,
white_king_square, black_king_square,
WHITE)
)
black_indices.append(
calculate_index(board.piece[square], board.color[square], square,
white_king_square, black_king_square,
BLACK)
)
So the function compute_active_indices is quite simple. We go through all pieces which aren’t a king that are on the board and for each one of them we calculate two indices, one from white’s and the other from black’s perspective.
The confusing part is the function calculate_index. It’s confusing because we want our function to be symmetrical with respect to the king’s perspective. So if the white king is in position E1 and there is a black bishop in position E3 we should output the same index as if we were looking at this from the other side’s perspective and there was a black king at position E8 and a white bishop in position E6. For this we have to change the orientation of a square when we’re looking at it from the black king’s perspective and also invert the piece_index array.
For each combination of (piece, color, square, king_square) there is a unique associated index.
The accumulator
The accumulator consists of two arrays of 256 elements. One array is filled using the indices we calculated from white’s perspective. The other from black’s perspective.
We’ll look at the code again and later explain what’s happenning:
# Here WHITE = 0 and BLACK = 1
def calculate_accumulator(list_of_indices):
accumulator = [[], []]
accumulator[WHITE] = ft_biases
accumulator[BLACK] = ft_biases
for index in list_of_indices[WHITE]:
accumulator[WHITE] += ft_weights[index * 256 : index * 256 + 256]
for index in list_of_indices[BLACK]:
accumulator[BLACK] += ft_weights[index * 256 : index * 256 + 256]
So each index tells us that a certain chunk of 256 elements of the weight array should be added to our accumulator.
Therefore you can think of all the possible indices as being the actual first layer of our network. If the index i is activated then the i-th node in our first layer is set to 1, otherwise to 0. And the weights connecting the i-th weight of the first layer with the first hidden layer are ft_weights[256 * i : 256 * i + 256].
You might think why we need so many input neurons. Why represent the board with a vector of 41024 elements containing just 1’s and 0’s? Why not use a more compact representation? I mean, we could just have 64 input neurons, one for each square.
Well, the answer to why the input is so sparse is that (1) it allows for efficient updates which is something we’ll talk about laer and (2) it turns out that the (piece, square, king square) representation provides a very meaningful piece of information to the network.
What do I mean by this? I’ll try to give an example because it’s very hard to distill what I mean into a sentence.
How meaningful is it to have a black queen at position A3? How much does it matter? To me it doesn’t sound like a very stimulating piece of information. Now the same question but with the king. How meaningful is it to have a white king at position A1? Does it tell you anything? Again, it doesn’t tell me anything particularly important. As isolated facts they aren’t quite interesting. But if we combine them, then we do get something interesting! A white king at A1 and a black queen at position A3, that’s possibly a checkmate! Probably at least a check! When we combined both pieces of information we turned them into something much more interesting.
The thing is that to it takes the neural net a lot of work to combine these two pieces of information. There have to be quite a lot of neurons working on detecting this situation, where a king is very close to the enemy queen on the corner of the board. On top of that, there have to be even more neurons working on interpreting this signal (is having a close enemy queen a good thing? or bad thing? or does it imply something else which is even more important? something like a checkmate?). So if we’re able to encode this as an input to our neural net we are saving it a lot of work. Now it just has to figure out what this signal means, but it doesn’t have to detect it. That’s kind of how I think about it.
Running the network
Now we pass this accumulator to our neural network. Two things will happen before we start running our matrix multiplications. We have to preprocess our accumulator. The result of this preprocessing is the input layer that we do matrix multiplications on.
Remember that our accumulator was made up of two 256-element arrays, one for white and one for black? Well, if it’s black’s turn then we will swap the two arrays. We do this because our neural net has to be side-agnostic. It calculates a value, which is big if the position is favorable for the side to move and negative otherwise, and it doesn’t matter if it’s black or white moving. It shouldn’t matter. We’re making the neural network’s life easier by not confusing it with the two different sides.
The other option would be to not swap the sides but multiply the resulting score by -1 if it’s black’s turn. However, it works better to keep it side agnostic. There can’t be any small bias towards either side, because the neural net just isn’t aware of which side is moving.
Also, the accumulator values will be clamped to a value from 0 to 127. Basically, if the value of the accumulator at a certain position is bigger than 127 it will be changed to be 127. If it’s smaller than 0 it will be changed to 0.
After these two steps it’s just like a classical neural network. After running each layer we divide the outputs by 64 and clamp them as we did before.
The efficiently updatable part
Suppose we were trying to optimize our neural net to make it run faster. One of the most important observations we could make is that between two runs of our evaluation function, the input is usually not that different.
When we’re searching millions of positions in our search function in an engine, we run the evaluation function in almost all the nodes we look at in the search tree. So me might run the evaluation function, then do some move, and then run it again. What changed in the accumulator? Not much. Just 2 indices in our active index list. So instead of recomputing again our accumulator from scratch we could just take the one we computed previously and update it. We’ll have to subtract the weights from the index that was previously there, and add those of the new index.
However, the rest of the network still has to be run. The only thing that changes is that you save time when computing the active indices and the accumulator.
So the reason why we overparametrize so much the accumulator, why we have 41024 parameters to fill a 256-element array is because we will rarely have to fill the accumulator from scratch but we will have to run the network every time. So it makes sense to try to make the accumulator as smart as we can. We don’t lose too much speed because of it.
Also, when a king is moved we’ll have to recompute at least half of the accumulator, since all the indices will change if the square of the king changes.
To be able to update the accumulator you have to remember the accumulator from previous positions and the movements you did from there to get to your current position. This is a bit more tricky to implement because to get maximum efficiency your accumulator history should be based on node depth. If I’m at a node at depth 5 (meaning my search function has done 5 moves to get to the current node) then I don’t care about the accumulator computed by other nodes at depth 5. I care about the accumulator computed at depth 4, because it’s the position that I come from.
Here you also have to decide how many accumulators in the past do you remember. The more you remember the more from-scratch accumulator updates you avoid. However, you also need much more space. I’ve found the optimal number for me is just 2, since >99% of the updates are performed with the last or the second-last accumulators.